いつものお店で追いコンでした．写真は本日のおすすめのサーロインです．

物理情報工学科では必修科目を中心に講義を撮影して動画の配信を行っています．いくつかはYouTubeを利用していますが，いくつかは学科のサーバーで配信しています．自前で配信すると履修者のみに視聴を限定するなどの自由度が高くなります．

慶應義塾大学には，授業支援のシステムとして，履修者のみに教材を配布する，あるいはレポート提出を電子的に行うものがあります．そこに動画配信の機能があればよいのですが，現状ではありません．動画配信の機能自体はあるようで，システムデザインマネージメント研究科のビデオや，PCの操作に関するビデオは配信されています．ある科目の履修者に配信する連携が用意されていません．

講義の動画配信の場合，本当のストリーミング配信にするべきであると考えています．ダウンロード型の配信では動画のファイルサイズが大きいためにダウンロードに時間がかかります．講義のビデオの配信には適していません．疑似ストリーミング配信では，視聴者の端末に動画のファイルが残ります．これはビデオの性質上，避けなければなりません．

自前で配信するために特別な予算はありません．サポートするための人員を増やせるわけでもありません．現状のスタッフで対応することになります．

これらのことから，Darwin Streaming Serverを使いました．Appleが無償で公開しているソフトウエアです．その代わり，配信できる動画の形式の制限が厳しく，また認証を使う必要もあって，動画投稿サイトのように簡単に動画をアップロードすることはできません．サポートするスタッフが対応できればよいレベルです．大学の授業支援のシステムで動画配信ができるようになるまでのつなぎです．

要旨には2つのスタイルがあります．一つは，問題を手短に述べて研究方法・結果・結論を記述するものです．報知的[1]あるいは情報型[2]と呼ばれるスタイルです．もう一つは，取り扱うテーマについて述べて結果を述べないものです．指示的[1]あるいは暗示型[2]と呼ばれるスタイルです．一つの論文誌の中でもシミュレーションの研究は指示的（暗示型）で，実験の研究は報知的（情報型）で書かれていることが多いように感じられます．

時制については，現在・過去・現在完了が一意的には定まっていない[1]，論文でなされている動作については現在形にする[1]，すでに終わった仕事を記述する意味合いで過去時制でかかれるべき[2]，結論の部分をのぞいて過去形で書く[3]，理論の論文では現在形だけですむこともある[1]， 実験の論文では be appleid, be studied, be measured は現在完了形が多い[1]，アブストラクトは自身の現在の研究結果を述べているので大抵の場合は過去時制にするべき[2]など様々です．

指示的（暗示型）であれば現在形が適切であると思います．一方，報知的（情報型）でかつ実験の研究あれば，目的と結論には現在形を，方法と結果には過去形を用いることが適切なように思います．しかし，出版社系のジャーナルに投稿する原稿を，ジャーナル名を記して英文校正会社に出したら，目的も過去形に修正されたことがあります．

[1] 平野進 編著：技術英文のすべて 第6版，丸善, 1983
[2] R. A. デイ，B. ガステル 著，美宅成樹 訳：世界に通じる科学英語論文の書き方，丸善, 2010
[3] 小野義正：ポイントで学ぶ科学英語論文の書き方，丸善, 2007

2月6日と7日に修士論文の発表会が開催されました．口頭発表で，発表12分＋質疑応答8分です．M2の秋に学会発表していますから発表の骨格はできています．データの追加や考察を深めてブラッシュアップすることになります．2年間の研究を12分にまとめますから，全てを話すことはできません．自分の研究の新規性・有効性・信頼性を示すことができること，（横断型の専修ですから）聴衆の専門分野に応じて（自分の分野の学会ではありませんから）適切な用語で説明できること，質問に適切に回答できる能力を問われます．

2月2日（土）と2月4日（月）に卒業研究発表会が開催されました．物理情報工学科では，研究の概要を発表する5分の口頭発表（質疑応答なし）と，ディスカッションを行うポスター発表の両方を行います．1期生のときからこの方式です．ディスカッションの時間を十分にとるためにポスター発表を，また4年生で卒業して社会に出る学生のことを考えれば口頭発表の経験を積むことも必要であるとの考えによります．

3日位前から急に海外からsshで不正にログインしようする攻撃が増えてきました．一日あたり3万から4万件です．日本人の名前のように読めるものもありますし，外国人の名前のように読めるものもあります．またシステムのサービス名もあります．以前は大学の入り口で，sshを短時間に連続して接続してくるものを弾いていたのですが，ポリシーが変わったのかも．

話は変わって，SMTP認証．2007年12月にサポートが終わったEudoraでSMTP認証を使えるようにするためには，サーバ側の調整がいろいろ必要なようでした．具体的なことはセキュリティに関わるので書けませんが，手元に記録を残しました．

プレアデス星団（すばる）

2次遅れ系の標準形
[latex]\displaystyle\frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}[/latex]

の共振周波数は，バネ・マス・ダッシュポットで構成される機械系の2次遅れ系の共振周波数と同様に求めることができます．LCR直列共振回路では，伝達関数の分子に[latex]s[/latex]がありますが，機械系には[latex]s[/latex]がなく分子は定数です．

形式的に[latex]s=j\omega[/latex]として
[latex]\displaystyle g(\omega)=\left|\frac{\omega_n^2}{\omega_n^2-\omega^2+j2\zeta\omega_n\omega}\right|[/latex]

になります．
[latex]\displaystyle\frac{dg(\omega)}{d\omega}=0[/latex]

を解くと
[latex]\displaystyle\omega_r=\omega_n\sqrt{1-2\zeta^2}[/latex]

になります．

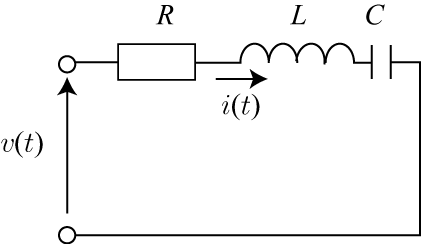
図のLCR直列共振回路では，電圧[latex]v(t)[/latex]を加えるときに流れる電流[latex]i(t)[/latex]は，
[latex]\displaystyle L\frac{i(t)}{dt}+Ri(t)+\frac{1}{C}\int i(t)dt=v(t)[/latex]

です．ラプラス変換して伝達関数[latex]G(s)=I(s)/V(s)[/latex]を求めると
[latex]\displaystyle G(s)=\frac{s}{Ls^2+Rs+1/C}[/latex]

になります．

形式的に[latex]s=j\omega[/latex]とおき，[latex]|G(j\omega)|=g(\omega)[/latex]とおくと
[latex]\displaystyle g(\omega)=\omega\left(\left(\frac{1}{c}-\omega^2L\right)^2+\omega^2R^2\right)^{-1/2}[/latex]

になります．

[latex]\displaystyle\frac{dg(\omega)}{d\omega}=0[/latex]として，極大値を求めると
[latex]\displaystyle\omega_r=\frac{1}{\sqrt{LC}}[/latex]になります（共振周波数は[latex]\displaystyle f_r=\frac{1}{2\pi\sqrt{LC}}[/latex]）．つまり，抵抗に依存しません．

計算で求めると煩雑ですが，LCR直列共振回路では複素平面でインピーダンスを表せば，Lのインピーダンス[latex]j\omega L[/latex]とCのインピーダンス[latex]\displaystyle\frac{1}{j\omega C}[/latex]の大きさが等しいときが共振の条件ですから容易に共振周波数を求められます．

一方，電圧源を短絡して電流の初期値のみを与えるとき，不足減衰であればその振動の角周波数は伝達関数の極の虚部から
[latex]\displaystyle\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}[/latex]

になります．

電気系では，「駆動力」である電圧と，「流れ」である電流に興味があります．力学系では「流れ」である速度ではなくその積分である変位で共振周波数を求めていることに注意が必要です．

外部から力を加えて強制的に振動させると，外部から加える力の周波数が共振周波数のときに振幅が最大になります．

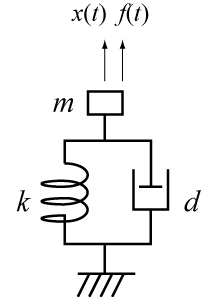
バネ・マス・ダッシュポットで構成される機械系の2次遅れ系に外力[latex]f(t)[/latex]を加えるときの変位[latex]x(t)[/latex]に関する微分方程式は
[latex]\displaystyle m\frac{d^2x}{dt^2}+d\frac{dx}{dt}+kx=f(t)[/latex]

になります．

ラプラス変換して伝達関数[latex]G(s)=X(s)/F(s)[/latex]を求めると
[latex]\displaystyle \frac{1}{ms^2+ds+k}[/latex]

になります．共振周波数はゲインが最大になる周波数ですから，形式的に[latex]s=j\omega[/latex]として，
[latex]\displaystyle |G(j\omega)|=\left|\frac{1}{-m\omega^2+j\omega ds + k}\right|[/latex]

になります．これを[latex]g(\omega)[/latex]とおくと
[latex]g(\omega)=((k-m\omega^2)^2+d^2\omega^2)^{-1/2}[/latex]

になります．

これが極大になる点を探せばよいので
[latex]\displaystyle\frac{dg(\omega)}{d\omega}=-\frac{1}{2}((k-m\omega^2)^2+d^2\omega^2)^{-3/2}(2(k-m\omega^2)(-2m\omega)+2d^2\omega)=0[/latex]

となり，これを解くと
[latex]\displaystyle\omega_r=\sqrt{\frac{k}{m}-\frac{d^2}{2m^2}}[/latex]

になります（共振周波数[latex]f_r=\omega_r/2\pi[/latex]）．

一方，零ではない初期値のみを与えて外力を加えない場合，不足減衰のときの振動の周波数（減衰固有周波数）は，伝達関数の極の虚部から
[latex]\displaystyle\frac{1}{2\pi}\sqrt{\frac{k}{m}-\frac{d^2}{4m^2}}[/latex]

になります．

機械系では，「駆動力」は外部から加えられる力で，「流れ」に対応するものは速度になります．しかし，興味があるのは変位ですから，「流れ」に対応する物理量を時間に関して積分した物理量になります．

2次遅れ系の伝達関数の標準形は
[latex]\displaystyle\frac{\omega_n^2}{s^2+2\zeta\omega_n+\omega_n^2}[/latex]

です．とくに断ることなく固有周波数というときには[latex]\omega_n/2\pi[/latex]のことを指します．減衰比[latex]\zeta[/latex]が零のときの固有周波数を明示的に区別して呼ぶときには，非減衰固有周波数あるいは不減衰固有周波数と呼びます．英語ではundamped natural frequecyです．また[latex]\zeta[/latex]が零ではないときの自由振動の周波数は，減衰固有周波数と呼ばれます．減衰固有周波数は，伝達関数の極から[latex]\displaystyle\frac{\omega_n\sqrt{1-\zeta^2}}{2\pi}[/latex]になります．