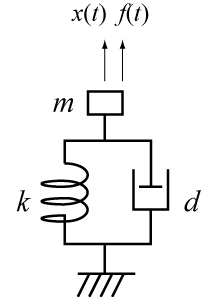
外部から力を加えて強制的に振動させると,外部から加える力の周波数が共振周波数のときに振幅が最大になります.
バネ・マス・ダッシュポットで構成される機械系の2次遅れ系に外力[latex]f(t)[/latex]を加えるときの変位[latex]x(t)[/latex]に関する微分方程式は
[latex]\displaystyle m\frac{d^2x}{dt^2}+d\frac{dx}{dt}+kx=f(t)[/latex]
になります.
ラプラス変換して伝達関数[latex]G(s)=X(s)/F(s)[/latex]を求めると
[latex]\displaystyle \frac{1}{ms^2+ds+k}[/latex]
になります.共振周波数はゲインが最大になる周波数ですから,形式的に[latex]s=j\omega[/latex]として,
[latex]\displaystyle |G(j\omega)|=\left|\frac{1}{-m\omega^2+j\omega ds + k}\right|[/latex]
になります.これを[latex]g(\omega)[/latex]とおくと
[latex]g(\omega)=((k-m\omega^2)^2+d^2\omega^2)^{-1/2}[/latex]
になります.
これが極大になる点を探せばよいので
[latex]\displaystyle\frac{dg(\omega)}{d\omega}=-\frac{1}{2}((k-m\omega^2)^2+d^2\omega^2)^{-3/2}(2(k-m\omega^2)(-2m\omega)+2d^2\omega)=0[/latex]
となり,これを解くと
[latex]\displaystyle\omega_r=\sqrt{\frac{k}{m}-\frac{d^2}{2m^2}}[/latex]
になります(共振周波数[latex]f_r=\omega_r/2\pi[/latex]).
一方,零ではない初期値のみを与えて外力を加えない場合,不足減衰のときの振動の周波数(減衰固有周波数)は,伝達関数の極の虚部から
[latex]\displaystyle\frac{1}{2\pi}\sqrt{\frac{k}{m}-\frac{d^2}{4m^2}}[/latex]
になります.
機械系では,「駆動力」は外部から加えられる力で,「流れ」に対応するものは速度になります.しかし,興味があるのは変位ですから,「流れ」に対応する物理量を時間に関して積分した物理量になります.