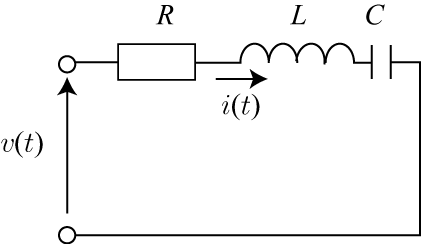
図のLCR直列共振回路では,電圧[latex]v(t)[/latex]を加えるときに流れる電流[latex]i(t)[/latex]は,
[latex]\displaystyle L\frac{i(t)}{dt}+Ri(t)+\frac{1}{C}\int i(t)dt=v(t)[/latex]
です.ラプラス変換して伝達関数[latex]G(s)=I(s)/V(s)[/latex]を求めると
[latex]\displaystyle G(s)=\frac{s}{Ls^2+Rs+1/C}[/latex]
になります.
形式的に[latex]s=j\omega[/latex]とおき,[latex]|G(j\omega)|=g(\omega)[/latex]とおくと
[latex]\displaystyle g(\omega)=\omega\left(\left(\frac{1}{c}-\omega^2L\right)^2+\omega^2R^2\right)^{-1/2}[/latex]
になります.
[latex]\displaystyle\frac{dg(\omega)}{d\omega}=0[/latex]として,極大値を求めると
[latex]\displaystyle\omega_r=\frac{1}{\sqrt{LC}}[/latex]になります(共振周波数は[latex]\displaystyle f_r=\frac{1}{2\pi\sqrt{LC}}[/latex]).つまり,抵抗に依存しません.
計算で求めると煩雑ですが,LCR直列共振回路では複素平面でインピーダンスを表せば,Lのインピーダンス[latex]j\omega L[/latex]とCのインピーダンス[latex]\displaystyle\frac{1}{j\omega C}[/latex]の大きさが等しいときが共振の条件ですから容易に共振周波数を求められます.
一方,電圧源を短絡して電流の初期値のみを与えるとき,不足減衰であればその振動の角周波数は伝達関数の極の虚部から
[latex]\displaystyle\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}[/latex]
になります.
電気系では,「駆動力」である電圧と,「流れ」である電流に興味があります.力学系では「流れ」である速度ではなくその積分である変位で共振周波数を求めていることに注意が必要です.