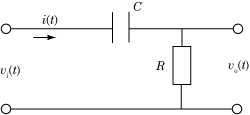
自然科学実験(物理学)のテーマ,オシロスコープの応用課題で特性を調べるローパスフィルタの抵抗とコンデンサを入れ替えて構成したハイパスフィルタです.
[latex]v_i(t) = \displaystyle\frac{1}{C}\int i(t) dt + v_o(t)[/latex]と[latex]v_o(t) = R i(t)[/latex]の関係がありますから,
[latex]v_i(t) = \displaystyle\frac{1}{RC}\int v_o(t) dt + v_o(t)[/latex]
になります.
ラプラス変換で解く
ラプラス変換して,
[latex]V_i(s) = \displaystyle\frac{V_o(s)}{RCs} + V_o(s)[/latex]
を得ます.伝達関数は
[latex]\displaystyle\frac{V_o(s)}{V_i(s)} = \frac{1}{\frac{1}{RCs} + 1} = \frac{s}{s+\frac{1}{RC}}[/latex]
になります.伝達関数の極は,抵抗とコンデンサを入れ替えて構成するローパスフィルタと同じになります.形式的に[latex]s=j\omega[/latex]とすると,ゲイン特性は
[latex]\left|\displaystyle\frac{V_o(s)}{V_i(s)}\right| = \displaystyle\frac{\omega}{\sqrt{\omega^2 + \left(\frac{1}{RC}\right)^2}}[/latex]
になります.
位相特性は
[latex]90^\circ – \tan^{-1}\omega RC[/latex]
になります.
1年生の数学の範囲で解く
同次微分方程式の解,つまり基本解は時間とともに零になるので,[latex]v_i(t)=\sin\omega t[/latex]のときの特解を求めればよいのは,ローパスフィルタの場合と同様です.
積分を含む式
[latex]v_i(t) = \displaystyle\frac{1}{RC}\int v_o(t) dt + v_o(t)[/latex]
なので,[latex]t[/latex]で微分して,
[latex]\displaystyle\frac{dv_i(t)}{dt}=\frac{1}{RC}v_o(t) + \frac{dv_o(t)}{dt}[/latex]
を得ます.[latex]\displaystyle\frac{dv_i(t)}{dt}=\omega\cos\omega t[/latex]を代入すると,
[latex]\omega\cos\omega t=\displaystyle\frac{1}{RC}v_o(t) + \frac{dv_o(t)}{dt}[/latex]
になります.[latex]v_o(t)[/latex]は,[latex]v_i(t)[/latex]と同じ角周波数の正弦波ですが,振幅と位相が異なるものになるので,解を[latex]a\sin(\omega t + \phi)[/latex]とおいて,[latex]a[/latex]と[latex]\phi[/latex] を求めます.
[latex]\omega\cos\omega t = \displaystyle\frac{1}{RC}a\sin(\omega t + \phi) + a\omega\cos(\omega t + \phi)[/latex]
になるので三角関数の合成を用いて,
[latex]\omega\cos\omega t = a\sqrt{\displaystyle\left(\frac{1}{RC}\right)^2 + \omega^2}\sin(\omega t + \phi + \psi)[/latex]
と
[latex]\psi=\tan^{-1}RC\omega[/latex]
となり,両辺を[latex]\cos[/latex]にして
[latex]\displaystyle\omega\cos\omega t = a\sqrt{\displaystyle\left(\frac{1}{RC}\right)^2 + \omega^2}\cos\left(-\frac{\pi}{2}+\omega t + \phi + \psi\right)[/latex]
となります.したがって
[latex]a=\displaystyle\frac{\omega}{\sqrt{\left(\frac{1}{RC}\right)^2 + \omega^2}}[/latex]
を得ます.
位相は[latex]\phi=\displaystyle\frac{\pi}{2}-\psi[/latex]なので,
[latex]90^\circ – \tan^{-1}RC\omega[/latex]
になります.