1年生の自然科学実験のテーマの一つにオシロスコープがあります.応用課題として,抵抗とコンデンサで作るローパスフィルタの周波数特性を計測する実験があります.1年生では電気回路の講義がなく,交流回路の解析はまだ習っていません.1年生の数学では非同次微分方程式の解き方を学ぶので,タイミングによっては数学的な説明ができます.それすらできないときには,コンデンサの性質を定性的に説明することになります.
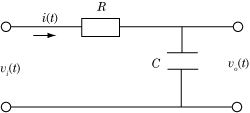
図の回路において,流れる電流を[latex]i(t)[/latex]とおくと,抵抗[latex]R[/latex]の部分の電圧は[latex]Ri(t)[/latex]です.コンデンサ[latex]C[/latex]の電圧は[latex]v_o(t)[/latex]です.また,[latex]i(t)=\displaystyle\frac{dv_o(t)}{dt}[/latex]です(この式は,[latex]Q=CV[/latex]と[latex]Q=\displaystyle\int i(t)dt[/latex]の関係で誘導しますが,高校の範囲では一定電流を[latex]\Delta t[/latex]流すと電荷が[latex]Q[/latex]になることまでで,積分では習っていないと思います).
[latex]v_i(t)=Ri(t) + v_o(t)[/latex]より,微分方程式[latex]v_i(t)=RC\displaystyle\frac{dv_o(t)}{dt} + v_o(t)[/latex]を得ます.
1年生の数学の範囲で解く
1年生の数学で,非同次微分方程式の解き方を学んでいれば,[latex]v_i(t)=0[/latex]のときの基本解は時間とともに減衰して零になるので,[latex]v_i(t)=\sin \omega t[/latex]のときの特解を求めればよいことが分ります.
特解は,この回路は線形系ですから,入力の正弦波と同じ周波数で振動するすけれども,振幅と位相が異なるだけになります.そこで解を[latex]a\sin(\omega t + \phi)[/latex]として,[latex]a[/latex]と[latex]\phi[/latex]を求めることにします.
微分方程式に代入すると,
[latex]\sin\omega t=RCa\omega\cos(\omega t + \phi) + a\sin(\omega t + \phi)[/latex]
になります.右辺に三角関数の合成を適用すると,
[latex]\sin\omega t = \sqrt{a^2 + (RCa\omega)^2}\sin(\omega t + \phi + \psi)[/latex]
になります.両辺の振幅を比較して
[latex]a=\displaystyle\frac{1}{\sqrt{1+(RC\omega)^2}}[/latex]
と,位相を比較して[latex]\phi = -\psi[/latex]から
[latex]\phi = -\tan^{-1}RC\omega[/latex]
を得ます.
交流回路の解析(フェーザ法)で解く
物理情報工学科では2年生春学期の電気回路同演習でフェーザ法を学びます.フェーザ法では,図の回路は
[latex]\dot{V_i} = R\dot{I} + \dot{V_o}[/latex]
と表すことができ,
[latex]\dot{V_o} =\displaystyle\frac{1}{j\omega C}\dot{I} [/latex]
を用いて[latex]\dot{I}[/latex]を消去すると,
[latex]\dot{V_i} = (j\omega RC + 1)\dot{V_o}[/latex]
を得ます.ゲイン特性は
[latex]\displaystyle\left|\frac{\dot{V_o}}{\dot{V_i}}\right| = \frac{1}{\sqrt{1 + (RC\omega)^2}}[/latex]
になります.
位相特性は
[latex]-\tan^{-1}RC\omega[/latex]
になります.
ラプラス変換で解く
物理情報工学科では2年生秋学期の物理情報数学Cでラプラス変換を学びます.ラプラス変換を学んでいれば,伝達関数に形式的に[latex]s=j\omega[/latex]としてゲイン特性と位相特性を求めることができます.
微分方程式をラプラス変換すると
[latex]V_o(s) = RCsV_i(s) + V_i(s)[/latex]
を得ます.伝達関数
[latex]\displaystyle\frac{V_o(s)}{V_i(s)} = \frac{1}{RCs + 1}[/latex]
を得ます.[latex]s=j\omega[/latex]とすれば,上記と同じゲイン特性と位相特性になります.
補足
実験を早く終わった学生には,入力波形を矩形波にして積分されている様子を観察することや,抵抗とコンデンサを入れ替えてハイパスフィルタにして,定性的にですが,ハイパスフィルタの特性や入力波(三角波)が微分されている様子を観察してもらっています.