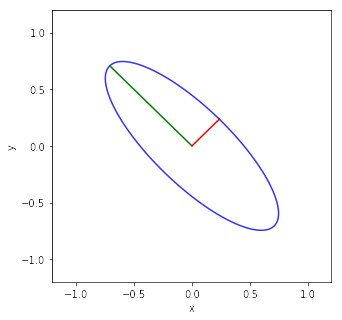
物理情報数学Bで対称行列の応用例として取り上げている傾いた楕円の式の説明です.
$5x^2 + 8xy + 5y^2 = 1$
の式を行列で表すと
$\left[\begin{array}{cc}x & y\end{array}\right]\left[\begin{array}{cc}5 & 4\\ 4 & 5\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=1$
になる.
行列を$A$と置くと,$A$の固有ベクトル(正規化されたもの)を列に持つ行列$Q$を用いて$A=Q\Lambda Q^T$と表せる.行列$A$は固有値として9と1を持つ.固有値が9のとき固有ベクトルは$[1\ 1]^T$である.固有値が1のとき固有ベクトルは$[1\ -1]^T$である.固有ベクトルの大きさは$\sqrt{2}$であるので
$\left[\begin{array}{cc}x & y\end{array}\right]\displaystyle\frac{1}{\sqrt{2}}\left[\begin{array}{rr}1 & 1\\ 1 & -1\end{array}\right]\left[\begin{array}{cc}9 & 0\\ 0 & 1\end{array}\right]\frac{1}{\sqrt{2}}\left[\begin{array}{rr}1 & 1\\ 1 & -1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=1$
となる.
この式は
$9\left(\displaystyle\frac{x+y}{\sqrt{2}}\right)^2 + 1\left(\displaystyle\frac{x-y}{\sqrt{2}}\right)^2=1$
と表せる.括弧内を$X$と$Y$と置くと,
$9X^2+Y^2=1$
の楕円の式になる.楕円の短半径は1/3で長半径は1になる.これらは,固有値の逆数の平方根である.
import numpy as np
import matplotlib.pyplot as plt
import numpy.linalg as LA
#
# 5x^2 + 8xy + 5y^2 = 1
# 9X^2 + y^2 = 1
# X = (x + y)/sqrt(2)
# Y = (x - y) /sqrt(2)
#
theta = np.arange(0, 361, 3)
X = np.cos(theta/180*np.pi)/3
Y = np.sin(theta/180*np.pi)
x = (X+Y)/np.sqrt(2)
y = (X-Y)/np.sqrt(2)
plt.figure(figsize=(5, 5))
plt.xlim([-1.2, 1.2])
plt.ylim([-1.2, 1.2])
plt.xlabel('x')
plt.ylabel('y')
plt.plot(x, y, color='blue', alpha=0.8)
#
A = np.array([[5, 4], [4, 5]])
w,v = LA.eig(A)
print('固有値')
print(w)
print('固有ベクトル')
print(v)
# 固有値の逆数の平方根が長半径と短半径
# 固有ベクトルが軸方向
a = v[:,0].reshape(2, 1) / np.sqrt(w[0])
b = v[:,1].reshape(2 ,1) / np.sqrt(w[1])
plt.plot(np.array([0, a[0]]), np.array([0, a[1]]), color='red')
plt.plot(np.array([0, b[0]]), np.array([0, b[1]]), color='green')
plt.show()
固有値 [9. 1.] 固有ベクトル [[ 0.70710678 -0.70710678] [ 0.70710678 0.70710678]]