当研究室では,ヒトを対象として,これまで計測することが難しかった物理量を推定する方法を研究しています.具体的には,生体の微小な信号を計測し,それを処理すること,またヒトに対する入力と出力を考えてそのシステムを同定することを行なっています.対象としては,次に述べる重心の動揺,筋が収縮するときの振動である筋音,筋が発生する力や,心臓から拍出された血液が拍動しながら血管を流れる様子を計測した脈波などです.
重心の動揺
ヒトの立位姿勢は,ヒトを足関節を回転軸とする倒立振子で図1のように表すことができます.ヒトの立位姿勢は,足関節周りの筋の粘弾性によって維持されています.ヒトが立位姿勢を維持しているときには,呼吸・心拍・内臓の運動や筋肉の収縮によって,重心の位置は図2のように常に揺らいでいます.呼吸・心拍・内臓の運動や筋肉の収縮を白色ノイズと仮定し,これが図3のように倒立振子に入力されていると考え,重心の揺らぎを倒立振子の出力と考えます.そうすると,入力と出力の間の伝達関数を推定すること(システムを同定すること)ができます.伝達関数を求めることができれば,倒立振子の運動方程式と合わせて,ヒトの足関節周りの弾性や粘性を知ることができます.
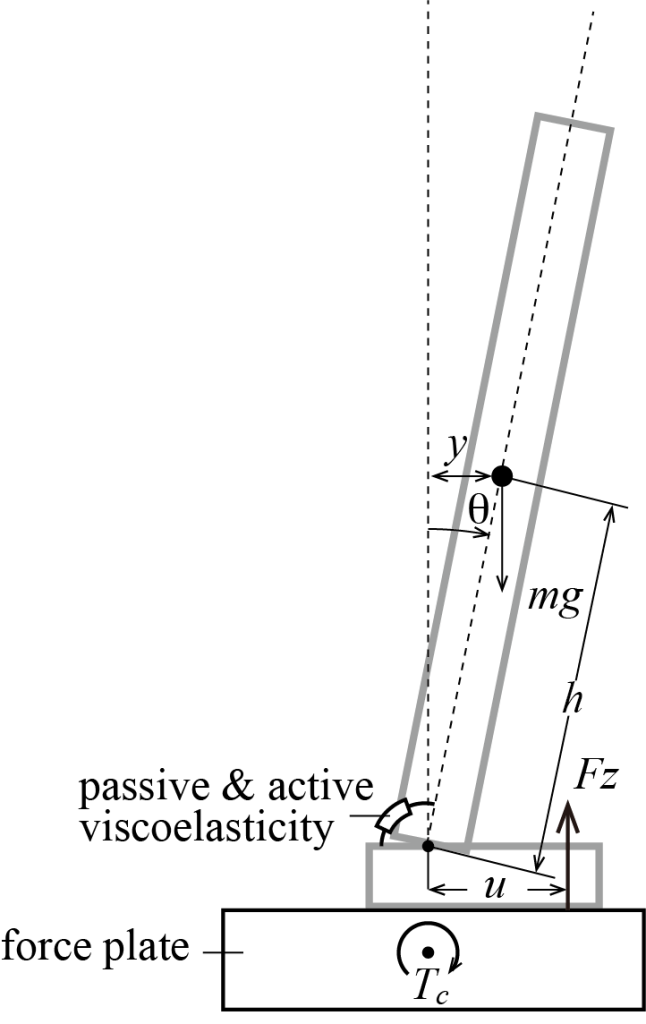
図1 ヒトの立位を倒立振子で表したモデル.
足関節周りの受動的・能動的粘弾性が立位を維持する.圧力中心の位置uをフィルタリングすると重心の位置yを得ることができる.ここで,mは体重,gは重力加速度,hは足関節の回転軸から重心までの長さ,θは足関節角度である.
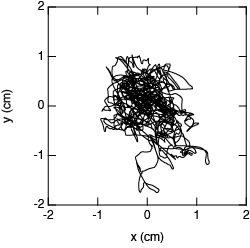
図2 立位姿勢を維持しているときの圧力中心のゆらぎ.
y軸が前後方向(+が前)
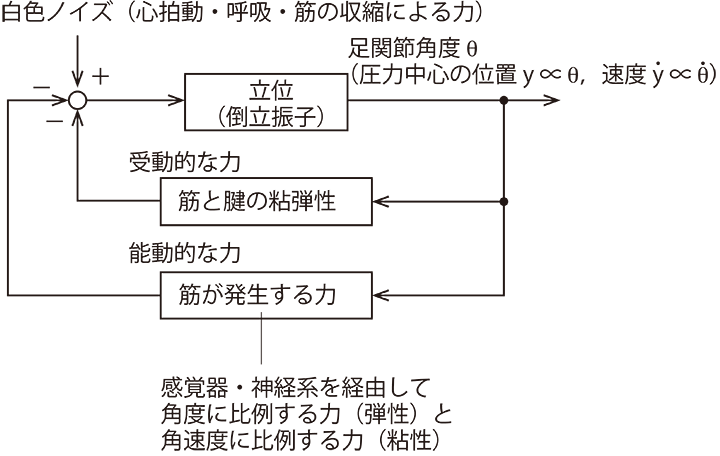
図3 ヒトの立位姿勢とフィードバックのブロック図.
筋と腱の受動的な粘弾性の他に,筋が発生する力も姿勢を安定化する.筋が発生する力は,足関節角度の変位と速度に比例すると仮定すると,能動的な粘弾性と考えることができる.
脈波
血管のモデルとしては,直感的で簡単な構造であり,動脈系をコンデンサと抵抗の組み合わせで表現し,血管のコンプライアンスと抵抗という生理学的に重要な特性を直接的に表していることから,集中定数系であるwindkesselモデルがしばしば脈波の解析に用いられます.例えば腕と手の血管を模式的に表すと図4 (a)のようになります.このwindkesselモデルを等価電気回路で表したものが図4 (b)です.この等価電気回路のPinとPoutの間の伝達関数は2次遅れ系になります.血管の圧力を非侵襲的に直接計ることはできませんが,脈波の振幅が血管の圧力に比例すると仮定すると,伝達関数からコンプライアンスや抵抗を知ることができます.
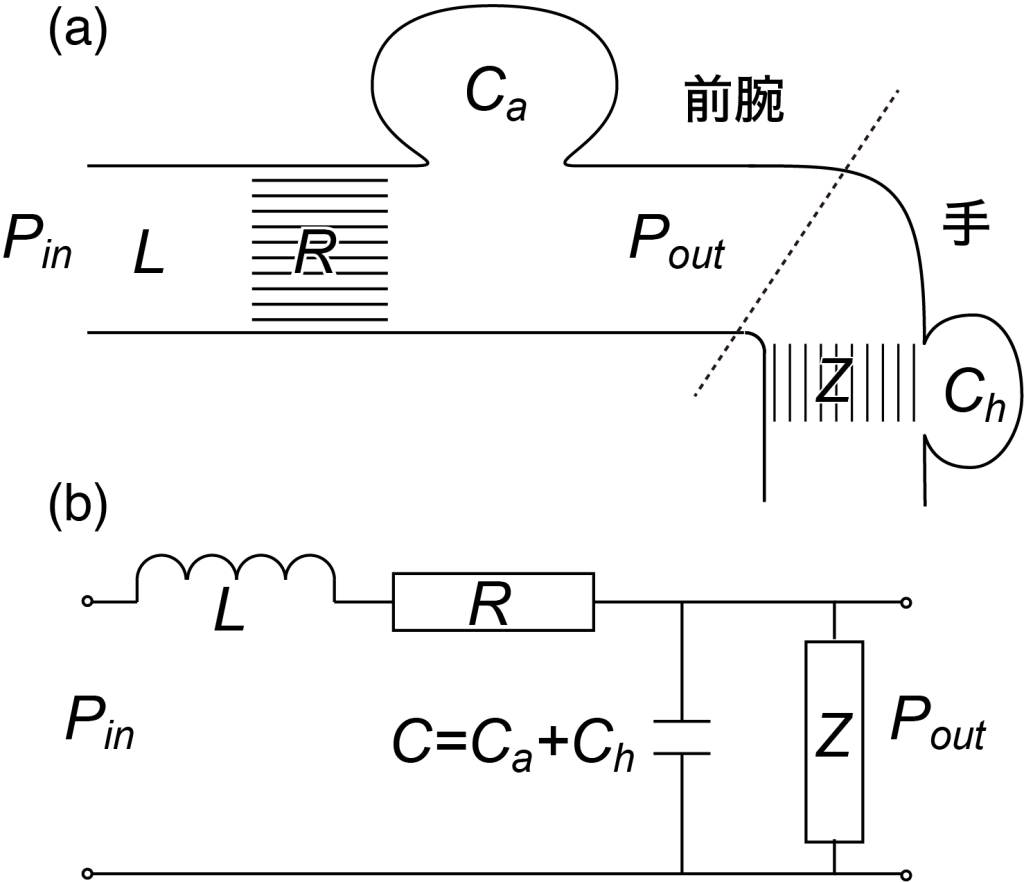
図4 腕と手の血管のwindkesselモデル.
CaとChはコンプライアンス.RとZは抵抗,PinとPoutは肘と手首の血管の圧力,Lは血液の慣性を表す.
