6月25日に，教授・准教授就任講演が開催されました．学科のweb pageの写真の多くは私が撮影しています．会場が14棟地下2Fのメルチメディアルームで暗いので，感度を上げて撮影しました．ISO 6400で撮影すれば，F4で1/200〜1/400 s程度で撮影できます．手ぶれ防止の機能のあるレンズを使いましたので，ぶれには更に強くなっています．3×3の配置にしたので講演者の写真3枚×2と，入り口の大看板，学部長が紹介している様子，それに日吉キャンパスの銀杏並木と図書館の間に植えられている紫陽花の写真を使いました．日吉から矢上キャンパスを撮影することも考えたのですが，生憎の曇り空でぱっとしないので止めました．
6月23日はスーパームーンの日でしたが，生憎の曇り空で月を撮影できませんでした．一日遅れの十六夜の月です．
RC回路の周波数特性を計測する実験のレポートで，理論値と実験値のずれに関する考察でオシロスコープの内部抵抗を原因の一つに上げているものがしばしばあります．結論から言えば，実験の回路ではオシロスコープの内部抵抗の影響は小さいです．
オシロスコープは電圧計です．理想的な電圧計では，電流が全く電圧計に流れないのですが，現実的には流れ込むため，理想的な電圧計とそれに並列な有限の抵抗で，現実の電圧計の等価回路を表します．オシロスコープの内部インピーダンスは1 MΩ程度です（プローブを使わないでリード線で配線しているので，10:1プローブを付けているときのように10 MΩ程度にはなりません）．それに対して実験に使っている回路の抵抗は10 kΩです．1/100ですから，影響は小さいです．むしろ抵抗やコンデンサの容量の誤差の方が大きいでしょう．
先日，広報用に撮影した写真の一部です．
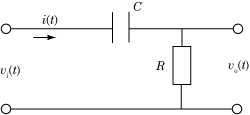
自然科学実験（物理学）のテーマ，オシロスコープの応用課題で特性を調べるローパスフィルタの抵抗とコンデンサを入れ替えて構成したハイパスフィルタです．
[latex]v_i(t) = \displaystyle\frac{1}{C}\int i(t) dt + v_o(t)[/latex]と[latex]v_o(t) = R i(t)[/latex]の関係がありますから，
[latex]v_i(t) = \displaystyle\frac{1}{RC}\int v_o(t) dt + v_o(t)[/latex]
になります．
ラプラス変換して，
[latex]V_i(s) = \displaystyle\frac{V_o(s)}{RCs} + V_o(s)[/latex]
を得ます．伝達関数は
[latex]\displaystyle\frac{V_o(s)}{V_i(s)} = \frac{1}{\frac{1}{RCs} + 1} = \frac{s}{s+\frac{1}{RC}}[/latex]
になります．伝達関数の極は，抵抗とコンデンサを入れ替えて構成するローパスフィルタと同じになります．形式的に[latex]s=j\omega[/latex]とすると，ゲイン特性は
[latex]\left|\displaystyle\frac{V_o(s)}{V_i(s)}\right| = \displaystyle\frac{\omega}{\sqrt{\omega^2 + \left(\frac{1}{RC}\right)^2}}[/latex]
になります．
位相特性は
[latex]90^\circ – \tan^{-1}\omega RC[/latex]
になります．
同次微分方程式の解，つまり基本解は時間とともに零になるので，[latex]v_i(t)=\sin\omega t[/latex]のときの特解を求めればよいのは，ローパスフィルタの場合と同様です．
積分を含む式
[latex]v_i(t) = \displaystyle\frac{1}{RC}\int v_o(t) dt + v_o(t)[/latex]
なので，[latex]t[/latex]で微分して，
[latex]\displaystyle\frac{dv_i(t)}{dt}=\frac{1}{RC}v_o(t) + \frac{dv_o(t)}{dt}[/latex]
を得ます．[latex]\displaystyle\frac{dv_i(t)}{dt}=\omega\cos\omega t[/latex]を代入すると，
[latex]\omega\cos\omega t=\displaystyle\frac{1}{RC}v_o(t) + \frac{dv_o(t)}{dt}[/latex]
になります．[latex]v_o(t)[/latex]は，[latex]v_i(t)[/latex]と同じ角周波数の正弦波ですが，振幅と位相が異なるものになるので，解を[latex]a\sin(\omega t + \phi)[/latex]とおいて，[latex]a[/latex]と[latex]\phi[/latex] を求めます．
[latex]\omega\cos\omega t = \displaystyle\frac{1}{RC}a\sin(\omega t + \phi) + a\omega\cos(\omega t + \phi)[/latex]
になるので三角関数の合成を用いて，
[latex]\omega\cos\omega t = a\sqrt{\displaystyle\left(\frac{1}{RC}\right)^2 + \omega^2}\sin(\omega t + \phi + \psi)[/latex]
と
[latex]\psi=\tan^{-1}RC\omega[/latex]
となり，両辺を[latex]\cos[/latex]にして
[latex]\displaystyle\omega\cos\omega t = a\sqrt{\displaystyle\left(\frac{1}{RC}\right)^2 + \omega^2}\cos\left(-\frac{\pi}{2}+\omega t + \phi + \psi\right)[/latex]
となります．したがって
[latex]a=\displaystyle\frac{\omega}{\sqrt{\left(\frac{1}{RC}\right)^2 + \omega^2}}[/latex]
を得ます．
位相は[latex]\phi=\displaystyle\frac{\pi}{2}-\psi[/latex]なので，
[latex]90^\circ – \tan^{-1}RC\omega[/latex]
になります．
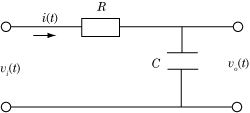
1年生の自然科学実験のテーマの一つにオシロスコープがあります．応用課題として，抵抗とコンデンサで作るローパスフィルタの周波数特性を計測する実験があります．1年生では電気回路の講義がなく，交流回路の解析はまだ習っていません．1年生の数学では非同次微分方程式の解き方を学ぶので，タイミングによっては数学的な説明ができます．それすらできないときには，コンデンサの性質を定性的に説明することになります．
図の回路において，流れる電流を[latex]i(t)[/latex]とおくと，抵抗[latex]R[/latex]の部分の電圧は[latex]Ri(t)[/latex]です．コンデンサ[latex]C[/latex]の電圧は[latex]v_o(t)[/latex]です．また，[latex]i(t)=\displaystyle\frac{dv_o(t)}{dt}[/latex]です（この式は，[latex]Q=CV[/latex]と[latex]Q=\displaystyle\int i(t)dt[/latex]の関係で誘導しますが，高校の範囲では一定電流を[latex]\Delta t[/latex]流すと電荷が[latex]Q[/latex]になることまでで，積分では習っていないと思います）．
[latex]v_i(t)=Ri(t) + v_o(t)[/latex]より，微分方程式[latex]v_i(t)=RC\displaystyle\frac{dv_o(t)}{dt} + v_o(t)[/latex]を得ます．
1年生の数学で，非同次微分方程式の解き方を学んでいれば，[latex]v_i(t)=0[/latex]のときの基本解は時間とともに減衰して零になるので，[latex]v_i(t)=\sin \omega t[/latex]のときの特解を求めればよいことが分ります．
特解は，この回路は線形系ですから，入力の正弦波と同じ周波数で振動するすけれども，振幅と位相が異なるだけになります．そこで解を[latex]a\sin(\omega t + \phi)[/latex]として，[latex]a[/latex]と[latex]\phi[/latex]を求めることにします．
微分方程式に代入すると，
[latex]\sin\omega t=RCa\omega\cos(\omega t + \phi) + a\sin(\omega t + \phi)[/latex]
になります．右辺に三角関数の合成を適用すると，
[latex]\sin\omega t = \sqrt{a^2 + (RCa\omega)^2}\sin(\omega t + \phi + \psi)[/latex]
になります．両辺の振幅を比較して
[latex]a=\displaystyle\frac{1}{\sqrt{1+(RC\omega)^2}}[/latex]
と，位相を比較して[latex]\phi = -\psi[/latex]から
[latex]\phi = -\tan^{-1}RC\omega[/latex]
を得ます．
物理情報工学科では2年生春学期の電気回路同演習でフェーザ法を学びます．フェーザ法では，図の回路は
[latex]\dot{V_i} = R\dot{I} + \dot{V_o}[/latex]
と表すことができ，
[latex]\dot{V_o} =\displaystyle\frac{1}{j\omega C}\dot{I} [/latex]
を用いて[latex]\dot{I}[/latex]を消去すると，
[latex]\dot{V_i} = (j\omega RC + 1)\dot{V_o}[/latex]
を得ます．ゲイン特性は
[latex]\displaystyle\left|\frac{\dot{V_o}}{\dot{V_i}}\right| = \frac{1}{\sqrt{1 + (RC\omega)^2}}[/latex]
になります．
位相特性は
[latex]-\tan^{-1}RC\omega[/latex]
になります．
物理情報工学科では2年生秋学期の物理情報数学Cでラプラス変換を学びます．ラプラス変換を学んでいれば，伝達関数に形式的に[latex]s=j\omega[/latex]としてゲイン特性と位相特性を求めることができます．
微分方程式をラプラス変換すると
[latex]V_o(s) = RCsV_i(s) + V_i(s)[/latex]
を得ます．伝達関数
[latex]\displaystyle\frac{V_o(s)}{V_i(s)} = \frac{1}{RCs + 1}[/latex]
を得ます．[latex]s=j\omega[/latex]とすれば，上記と同じゲイン特性と位相特性になります．
実験を早く終わった学生には，入力波形を矩形波にして積分されている様子を観察することや，抵抗とコンデンサを入れ替えてハイパスフィルタにして，定性的にですが，ハイパスフィルタの特性や入力波（三角波）が微分されている様子を観察してもらっています．
学科のパンフレットをはじめとする広報用の撮影日でした．撮影はプロのカメラマンにお願いしています．当研究室では，ヒトを計ることを行っており，運動中の筋肉の特性をシステム同定のテクニックを用いて明らかにしています．特徴的な被写体として，自転車エルゴメータとトレッドミルを選びました．また，学生のディスカッション風景なども撮影しました．撮影した写真のいくつかが採用されることを期待しています．
本研究室のようにヒトを被験者として研究を行う場合には生命倫理について意識しなければなりません．工学系の研究に適用し易い倫理指針がなくて苦労したのですが，数年前に日本人間工学会から，人間工学研究のための倫理指針が公開されました．それを含めて以下の生命倫理に関するweb pageをリンクのページに追加しました．
いつものお店で4年生の歓迎会でした．ここ2年間の卒業研究のテーマは筋音関連でしたけれど，今年度は日吉の体育研究所との共同研究のテーマを再開します．写真は本日のお勧めのマキ（肩ロースからリブロースにかけての芯ロースの周りを巻いている部分のようです）です．
9月12日〜14日に，日吉キャンパスにて計測自動制御学会ライフエンジニアリング部門シンポジウム2013が開催されます（http://le2013.l-bmi.org）．筋音のオーガナイズドセッションを計画中です．
