物理情報数学Bで扱った行列AをA=UΣVTに特異値分解します.
#
import numpy as np
import matplotlib.pyplot as plt
A = np.array([[2, 2], [-1, 2]])
U, S, V = np.linalg.svd(A) # V^TがVに入ることに注意する
print("特異値分解")
print("U")
print(U)
print("S")
print(S)
print("V")
print(V)
print("USV^T")
S2 = np.eye(2)*S
#
plt.figure(figsize=(5, 5))
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.xlabel('x1')
plt.ylabel('x2')
print(np.dot(np.dot(U, S2), V))
#
theta = np.arange(0, 361, 3)
uc = np.array([np.cos(theta/180*np.pi), np.sin(theta/180*np.pi)])
#
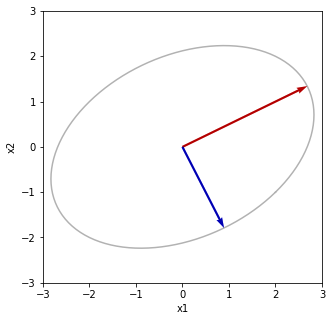
print("Vの列ベクトルと単位円")
plt.plot(uc[0,:], uc[1,:], color='black', alpha=0.3)
plt.quiver(0, 0, V[0, 0], V[0, 1], angles="xy", scale_units='xy', scale=1, color='red')
plt.quiver(0, 0, V[1, 0], V[1, 1], angles="xy", scale_units='xy', scale=1, color='blue')
plt.show()
x1 = np.dot(V, V.T)
c1 = np.dot(V, uc)
print("Vの列をV^Tで写像する V^TV 回転と鏡映")
print(x1)
plt.figure(figsize=(5, 5))
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.xlabel('x1')
plt.ylabel('x2')
plt.plot(c1[0,:], c1[1,:], color='black', alpha=0.3)
plt.quiver(0, 0, x1[0, 0], x1[1, 0], angles="xy", scale_units='xy', scale=1, color='red')
plt.quiver(0, 0, x1[0, 1], x1[1, 1], angles="xy", scale_units='xy', scale=1, color='blue')
plt.show()
print("それをシグマで写像する ΣV^TV 軸方向に拡大・縮小(特異値倍)する")
x2 = np.dot(S2, x1 )
c2 = np.dot(S2, c1)
print(x2)
plt.figure(figsize=(5, 5))
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.xlabel('x1')
plt.ylabel('x2')
plt.plot(c2[0,:], c2[1,:], color='black', alpha=0.3)
plt.quiver(0, 0, x2[0, 0], x2[1, 0], angles="xy", scale_units='xy', scale=1, color='red')
plt.quiver(0, 0, x2[0, 1], x2[1, 1], angles="xy", scale_units='xy', scale=1, color='blue')
plt.show()
print("最後にUで写像する UΣV^TV 回転と鏡映")
print("u1とu2のσ1倍とσ2倍にそれぞれ重なる")
x3 = np.dot(U, x2)
c3 = np.dot(U, c2)
print(x3)
plt.figure(figsize=(5, 5))
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.xlabel('x1')
plt.ylabel('x2')
plt.plot(c3[0,:], c3[1,:], color='black', alpha=0.3)
plt.quiver(0, 0, x3[0, 0], x3[1, 0], angles="xy", scale_units='xy', scale=1, color='red')
plt.quiver(0, 0, x3[0, 1], x3[1, 1], angles="xy", scale_units='xy', scale=1, color='blue')
plt.quiver(0, 0, S[0]*U[0, 0], S[0]*U[1, 0], angles="xy", scale_units='xy', scale=1, color='black', alpha=0.3)
plt.quiver(0, 0, S[1]*U[0, 1], S[1]*U[1, 1], angles="xy", scale_units='xy', scale=1, color='black', alpha=0.3)
plt.show()
特異値分解 U [[ 0.89442719 0.4472136 ] [ 0.4472136 -0.89442719]] S [3. 2.] V [[ 0.4472136 0.89442719] [ 0.89442719 -0.4472136 ]] USV^T [[ 2. 2.] [-1. 2.]] Vの列ベクトルと単位円
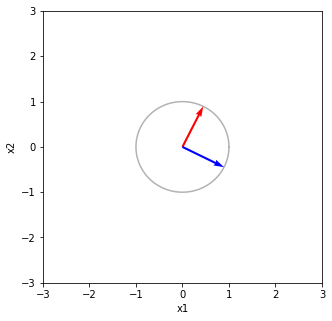
Vの列をV^Tで写像する V^TV 回転と鏡映 [[ 1.00000000e+00 -2.43158597e-17] [-2.43158597e-17 1.00000000e+00]]
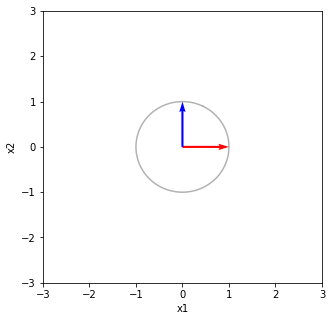
それをシグマで写像する ΣV^TV 軸方向に拡大・縮小(特異値倍)する [[ 3.00000000e+00 -7.29475792e-17] [-4.86317195e-17 2.00000000e+00]]
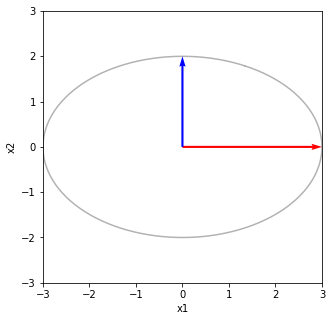
最後にUで写像する UΣV^TV 回転と鏡映 u1とu2のσ1倍とσ2倍にそれぞれ重なる [[ 2.68328157 0.89442719] [ 1.34164079 -1.78885438]]