餌と捕食者の関係

物理情報数学Bで，行列の累乗の応用例として，餌と捕食者の関係を表す行列差分方程式を説明しています．

「第[latex]k[/latex]年のイワシの数を[latex]x_1(k)[/latex]，クジラの数を[latex]x_2(k)[/latex]とする．クジラがいないときの1年後のイワシの数を[latex]\alpha x_1(k)[/latex]とする．つまり，第[latex]k[/latex]年のイワシの数に比例して変化する．クジラに1年間に食べられるイワシの数を[latex]\beta x_2(k)[/latex]とする．つまり，クジラの数に比例するイワシが食べられる．イワシがいないときの1年後のクジラの数を[latex]\gamma x_2(k)[/latex]とする．また，イワシを食べて1年間に増加するクジラの数を[latex]\delta x_1(k)[/latex]とする．」

上記の関係を行列差分方程式で表すと

[latex]

\left[\begin{array}{c}x_1(k+1) \\x_2(k+2)\end{array}\right]

=

\left[\begin{array}{rr}\alpha & -\beta \\ \delta & \gamma\end{array}\right]

\left[\begin{array}{c}x_1(k) \\x_2(k)\end{array}\right]

[/latex]

になります．一般解は

[latex]\boldsymbol{x}(k) = \left[\begin{array}{rr}\alpha & -\beta \\ \delta & \gamma\end{array}\right]^k\boldsymbol{x}(0)[/latex]

になります．

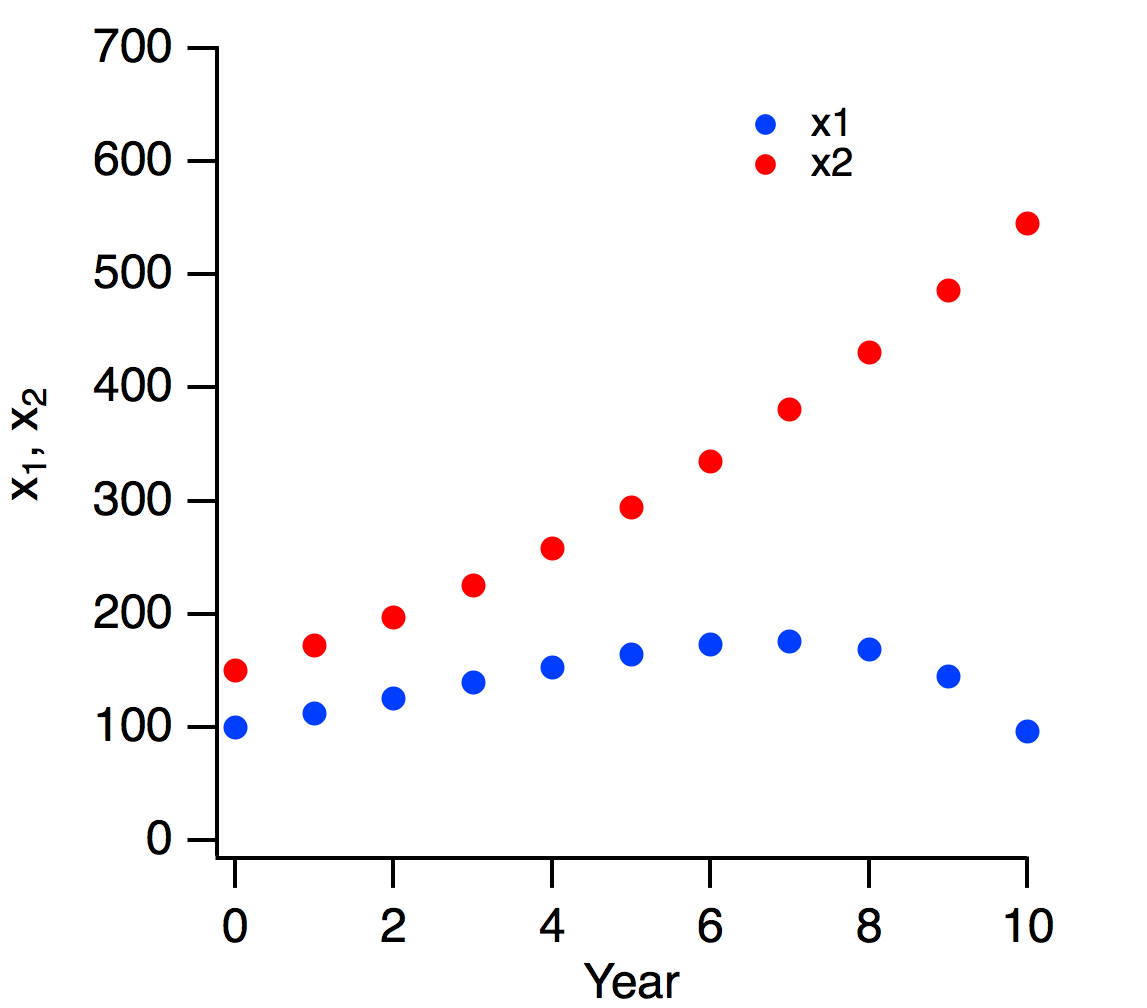
この行列差分方程式を講義では手計算で解けるように，[latex]\alpha=1.5[/latex]，[latex]\beta=0.25[/latex]，[latex]\gamma=1.1[/latex]，[latex]\delta=0.07[/latex]として解きます．しかし，この行列の固有値は1以上の実数が2つですので，餌と捕食者の数の変化に期待される振動的な振る舞いにはなりません．初期値のクジラの数が多いと，下図のようにイワシの数は減少に転じます．

餌と捕食者の関係のモデルとしては，ロトカ・ボルテラのモデルが知られています．このモデルでは，

[latex]

\displaystyle\frac{dx_1(t)}{dt} = \alpha x_1(t) – \beta x_1(t)x_2(t) \\

\displaystyle\frac{dx_2(t)}{dt} = \delta x_1(t)x_2(t) – \gamma x_2(t)

[/latex]

で表されます．非線形微分方程式ですから，[latex]x_1(t)[/latex]と[latex]x_2(t)[/latex]を解析的に求めることはできません．適当な値を代入して数値解を求めると，[latex]x_1(t)[/latex]と[latex]x_2(t)[/latex]が振動的な振る舞いをすることがわかります．

また，平衡点は[latex]dx_1(t)/dt=0[/latex]と[latex]dx_2(t)/dt=0[/latex]から，原点と[latex]x_1=\gamma/\delta[/latex]，[latex]x_2=\alpha/\beta[/latex]にあります．平衡点近傍では，[latex]x_1(t)x_2(t)[/latex]の項が小さいので無視できると仮定すると，[latex](0, 0)[/latex]の平衡点近傍では，

[latex]

\displaystyle\frac{d}{dt}\left[\begin{array}{c}x_1(t) \\x_2(t)\end{array}\right]

=

\left[\begin{array}{rr}\alpha & 0 \\

0 & -\gamma\end{array}\right]

\left[\begin{array}{c}x_1(t) \\x_2(t)\end{array}\right]

[/latex]

となり，行列の固有値は実数で1つは正でもう1つは負です．したがって，[latex](0, 0)[/latex]は鞍点です．

また，もう1つの平衡点[latex](\gamma/\delta, \alpha/\beta)[/latex]の近傍では，[latex]x_1(t)[/latex]を[latex]x_1+\gamma/\delta[/latex]，[latex]x_2(t)[/latex]を[latex]x_2+\alpha/\beta[/latex]とおいて，[latex]x_1(t)x_2(t)[/latex]の項が小さいので無視できると仮定すると

[latex]

\displaystyle\frac{d}{dt}\left[\begin{array}{c}x_1(t) \\x_2(t)\end{array}\right]

=

\left[\begin{array}{rr}0 & -\frac{\beta\gamma}{\delta} \\

\frac{\alpha\delta}{\beta} & 0\end{array}\right]

\left[\begin{array}{c}x_1(t) \\x_2(t)\end{array}\right]

[/latex]

と表されます．したがって，固有値が純虚数となり，振動する解になります．

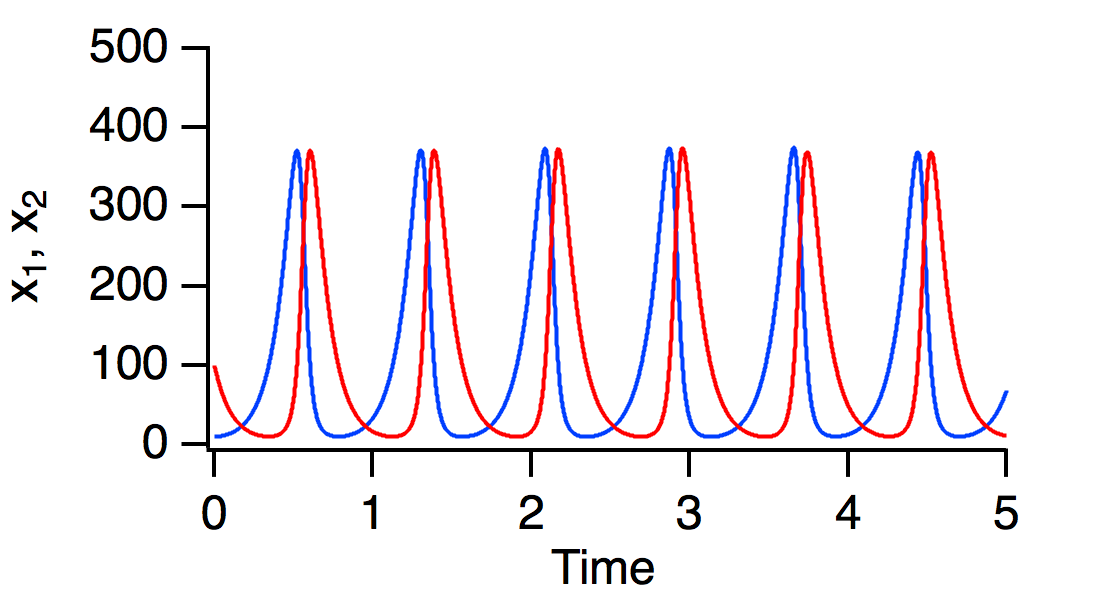
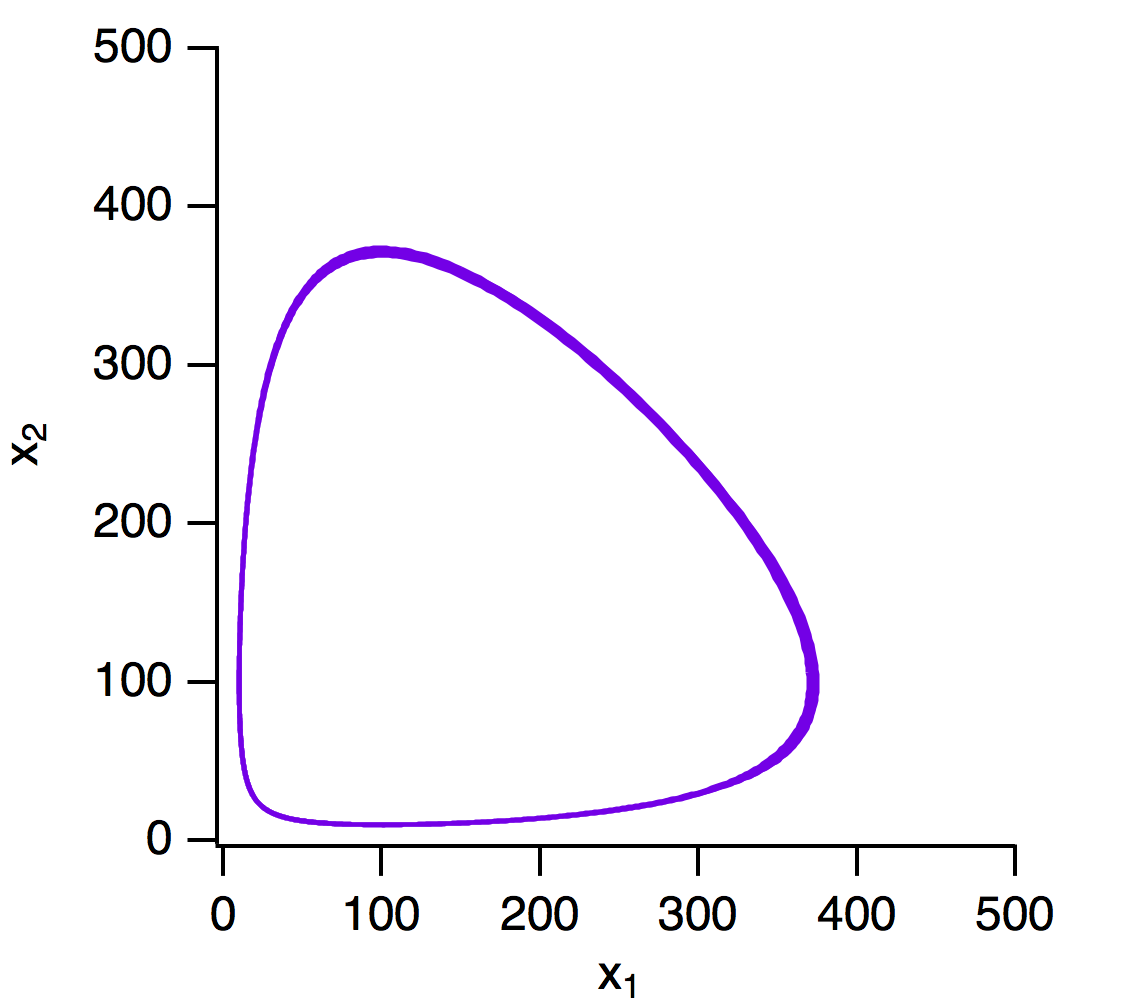
[latex]\alpha=10[/latex]，[latex]\beta=0.1[/latex]，[latex]\gamma=10[/latex]，[latex]\delta=0.1[/latex]とし，[latex]x_1(0)=10[/latex]と[latex]x_2(0)=100[/latex] で数値解を求めると下図のようになります．上のパネルは[latex]x_1(t)[/latex]と[latex]x_2(t)[/latex]の時間発展です． 下のパネルは[latex]x_1(t)[/latex]と[latex]x_2(t)[/latex]の関係です．

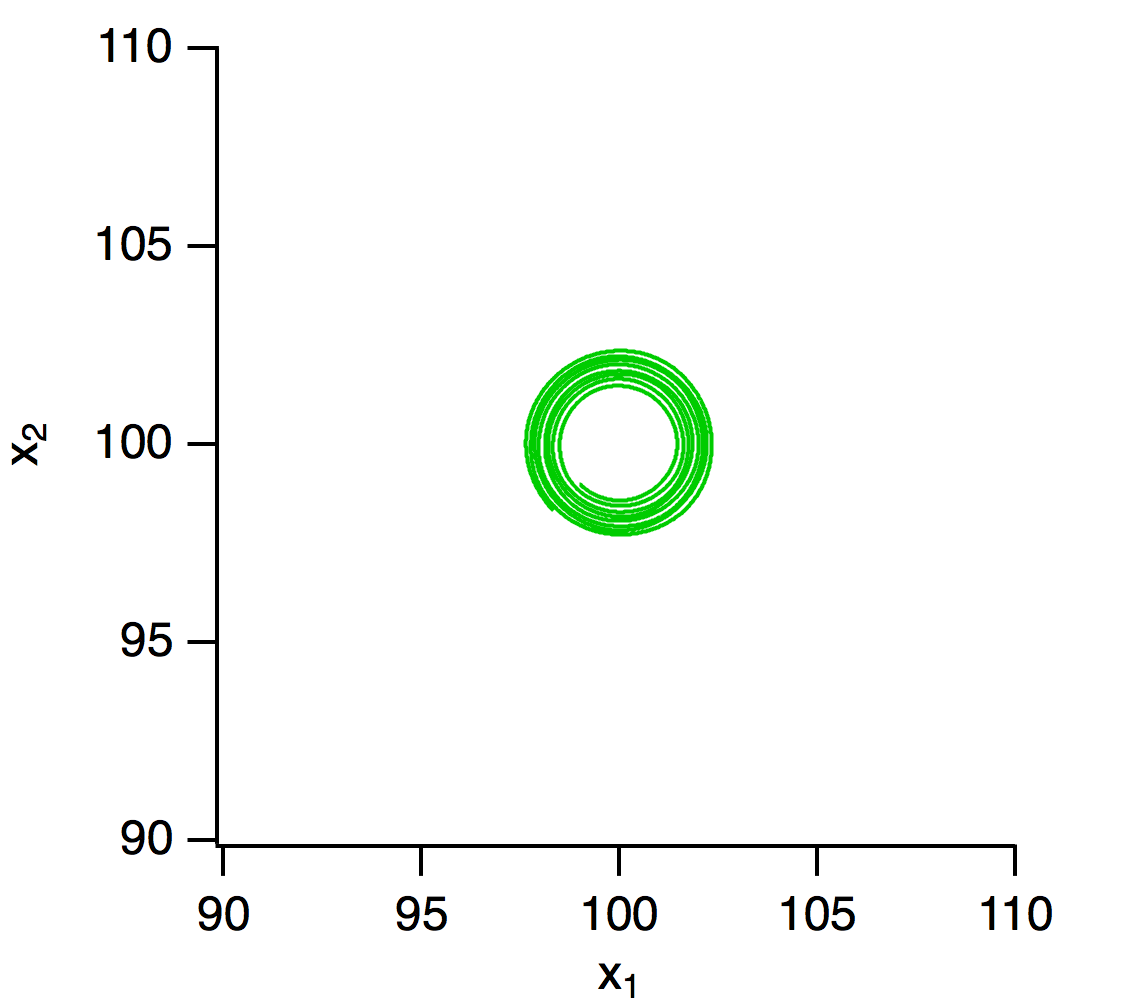
初期値を平衡点（(100, 100)）に近い点(99, 99)とすると下図のように円に近い軌道を描きます．

MATLABのコードです．

• lv.m

tspan = [0:0.001:5];
[t y] = ode45(@LotkaVolterra,tspan, [99 99]);
figure(1);
plot(t, y(:,1), 'b', t, y(:,2), 'r');
figure(2);
plot(y(:,1), y(:,2));

• LotkaVolterra.m

function dx = LotkaVolterra(t, x)
alpha = 10;
beta = 0.1;
gamma = 10;
delta = 0.1;
dx = zeros(2,1);
dx(1) = alpha * x(1) - beta * x(1) * x(2);
dx(2) = delta * x(1) * x(2) - gamma * x(2);
end