日光でした．集合写真は隠れ三滝です．

残念ながら，電子工学科の田邉研に大差で負けました．

論文賞
Takanori Uchiyama, Takahiro Tamura: System identification of mechanomyogram at various levels of motor unit recruitment, SICE JCMSI Vol. 7, No. 6

著述賞
福岡豊，内山孝憲，野村泰伸：生体システム工学の基礎，コロナ社，2015年

2件を受賞しました．

論文賞の対象論文は，田村の修士論文をまとめたものです．著述賞の書籍は，3年生の選択科目のバイオシステムの教科書です．

プレゼンテーション技法の講義の一環として，卒業研究の中間発表会が開催されました．当研究室の石川がbest presenterの一人に選ばれました．

塾内高校生のための慶應義塾大学理工学部夏休み研究体験のコース「筋肉のしなやかさを測ろう」を実施しました．慶應高校から1名，湘南藤沢高校から1名が参加しました．無酸素運動能力テストの一つであるウィンゲートテストを実施し，その前後で外側広筋の硬さを筋緊張計で計測しました．4年生が説明の補助を担当しました．

ウィンゲートテスト中

筋緊張計の計測データの解析

データの解析では，筋緊張計に内蔵されているソフトウエアを用いずに，システム同定の考え方に基づいて指数関数的に減衰する振動の周波数と時定数から，スティフネスを求めました．

春学期の打ち上げでした．そうは言っても，まだM2の中間発表会や，期末試験に期末レポートが残っています．打ち上げはいつもの焼肉です．

木星を観測しやすい季節になりました．また，月末には火星が接近します．口径80 mmの屈折式望遠鏡にカメラを取り付けてリレーレンズ方式で撮影しました．

バイオメカニズム学会誌の特集「柔軟物の硬さ」を担当しました．Vol. 40, No. 2として5月1日に発行されました．特集では，

• 内山，永岡：押し込み型の硬度計，バイオメカニズム学会誌，Vol. 40, No. 2, pp. 97-102, (2016)

を寄稿しました．押し込み型の硬度計の計測原理と，ウレタンフォームなど様々な柔軟物を市販の硬度計で計測したときの指示値間の関係について解説しました．用いた硬度計は，アスカーゴム硬度計E型（高分子計器株式会社），PEK-1（株式会社井元製作所），TDM-Z1（有限会社トライオール），FGRT-5（日本電算シンポ株式会社），TK-03C（株式会社特殊計測）の5機種です．

物理情報数学Bで，行列の累乗の応用例として，餌と捕食者の関係を表す行列差分方程式を説明しています．

「第[latex]k[/latex]年のイワシの数を[latex]x_1(k)[/latex]，クジラの数を[latex]x_2(k)[/latex]とする．クジラがいないときの1年後のイワシの数を[latex]\alpha x_1(k)[/latex]とする．つまり，第[latex]k[/latex]年のイワシの数に比例して変化する．クジラに1年間に食べられるイワシの数を[latex]\beta x_2(k)[/latex]とする．つまり，クジラの数に比例するイワシが食べられる．イワシがいないときの1年後のクジラの数を[latex]\gamma x_2(k)[/latex]とする．また，イワシを食べて1年間に増加するクジラの数を[latex]\delta x_1(k)[/latex]とする．」

上記の関係を行列差分方程式で表すと

[latex]

\left[\begin{array}{c}x_1(k+1) \\x_2(k+2)\end{array}\right]

=

\left[\begin{array}{rr}\alpha & -\beta \\ \delta & \gamma\end{array}\right]

\left[\begin{array}{c}x_1(k) \\x_2(k)\end{array}\right]

[/latex]

になります．一般解は

[latex]\boldsymbol{x}(k) = \left[\begin{array}{rr}\alpha & -\beta \\ \delta & \gamma\end{array}\right]^k\boldsymbol{x}(0)[/latex]

になります．

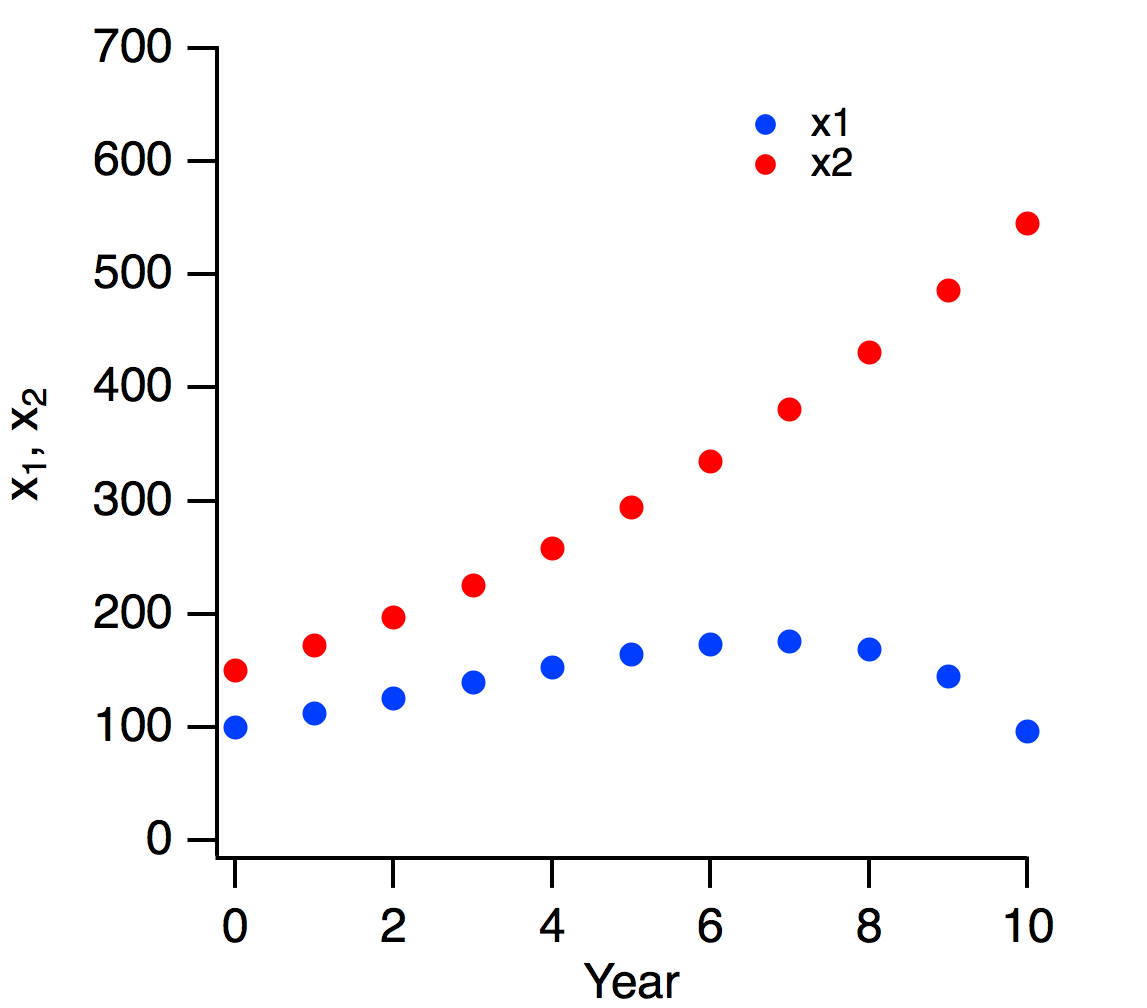
この行列差分方程式を講義では手計算で解けるように，[latex]\alpha=1.5[/latex]，[latex]\beta=0.25[/latex]，[latex]\gamma=1.1[/latex]，[latex]\delta=0.07[/latex]として解きます．しかし，この行列の固有値は1以上の実数が2つですので，餌と捕食者の数の変化に期待される振動的な振る舞いにはなりません．初期値のクジラの数が多いと，下図のようにイワシの数は減少に転じます．

餌と捕食者の関係のモデルとしては，ロトカ・ボルテラのモデルが知られています．このモデルでは，

[latex]

\displaystyle\frac{dx_1(t)}{dt} = \alpha x_1(t) – \beta x_1(t)x_2(t) \\

\displaystyle\frac{dx_2(t)}{dt} = \delta x_1(t)x_2(t) – \gamma x_2(t)

[/latex]

で表されます．非線形微分方程式ですから，[latex]x_1(t)[/latex]と[latex]x_2(t)[/latex]を解析的に求めることはできません．適当な値を代入して数値解を求めると，[latex]x_1(t)[/latex]と[latex]x_2(t)[/latex]が振動的な振る舞いをすることがわかります．

また，平衡点は[latex]dx_1(t)/dt=0[/latex]と[latex]dx_2(t)/dt=0[/latex]から，原点と[latex]x_1=\gamma/\delta[/latex]，[latex]x_2=\alpha/\beta[/latex]にあります．平衡点近傍では，[latex]x_1(t)x_2(t)[/latex]の項が小さいので無視できると仮定すると，[latex](0, 0)[/latex]の平衡点近傍では，

[latex]

\displaystyle\frac{d}{dt}\left[\begin{array}{c}x_1(t) \\x_2(t)\end{array}\right]

=

\left[\begin{array}{rr}\alpha & 0 \\

0 & -\gamma\end{array}\right]

\left[\begin{array}{c}x_1(t) \\x_2(t)\end{array}\right]

[/latex]

となり，行列の固有値は実数で1つは正でもう1つは負です．したがって，[latex](0, 0)[/latex]は鞍点です．

また，もう1つの平衡点[latex](\gamma/\delta, \alpha/\beta)[/latex]の近傍では，[latex]x_1(t)[/latex]を[latex]x_1+\gamma/\delta[/latex]，[latex]x_2(t)[/latex]を[latex]x_2+\alpha/\beta[/latex]とおいて，[latex]x_1(t)x_2(t)[/latex]の項が小さいので無視できると仮定すると

[latex]

\displaystyle\frac{d}{dt}\left[\begin{array}{c}x_1(t) \\x_2(t)\end{array}\right]

=

\left[\begin{array}{rr}0 & -\frac{\beta\gamma}{\delta} \\

\frac{\alpha\delta}{\beta} & 0\end{array}\right]

\left[\begin{array}{c}x_1(t) \\x_2(t)\end{array}\right]

[/latex]

と表されます．したがって，固有値が純虚数となり，振動する解になります．

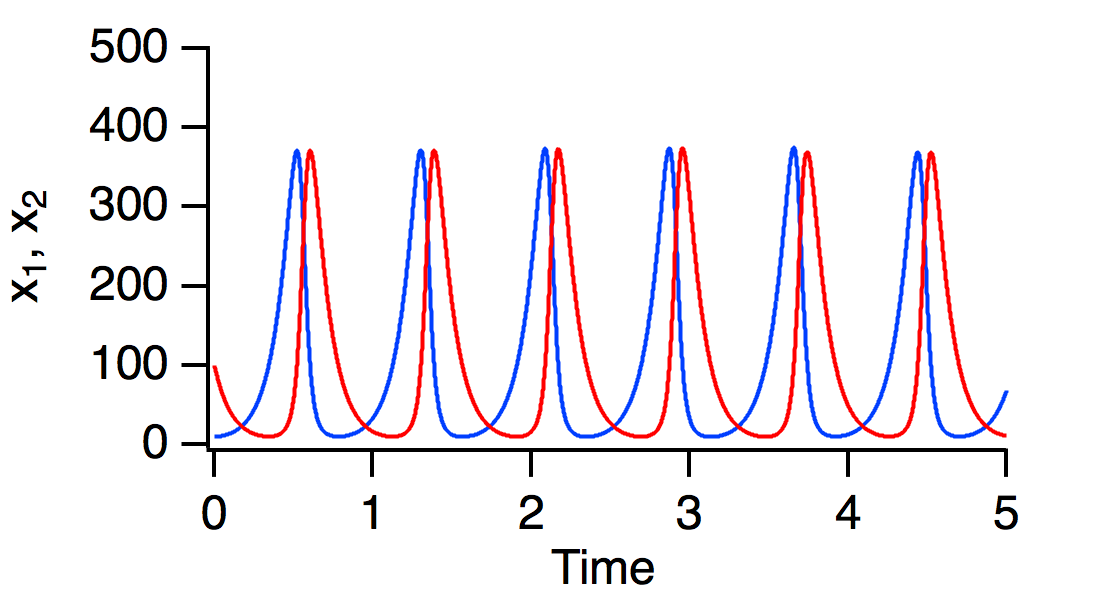
[latex]\alpha=10[/latex]，[latex]\beta=0.1[/latex]，[latex]\gamma=10[/latex]，[latex]\delta=0.1[/latex]とし，[latex]x_1(0)=10[/latex]と[latex]x_2(0)=100[/latex] で数値解を求めると下図のようになります．上のパネルは[latex]x_1(t)[/latex]と[latex]x_2(t)[/latex]の時間発展です． 下のパネルは[latex]x_1(t)[/latex]と[latex]x_2(t)[/latex]の関係です．

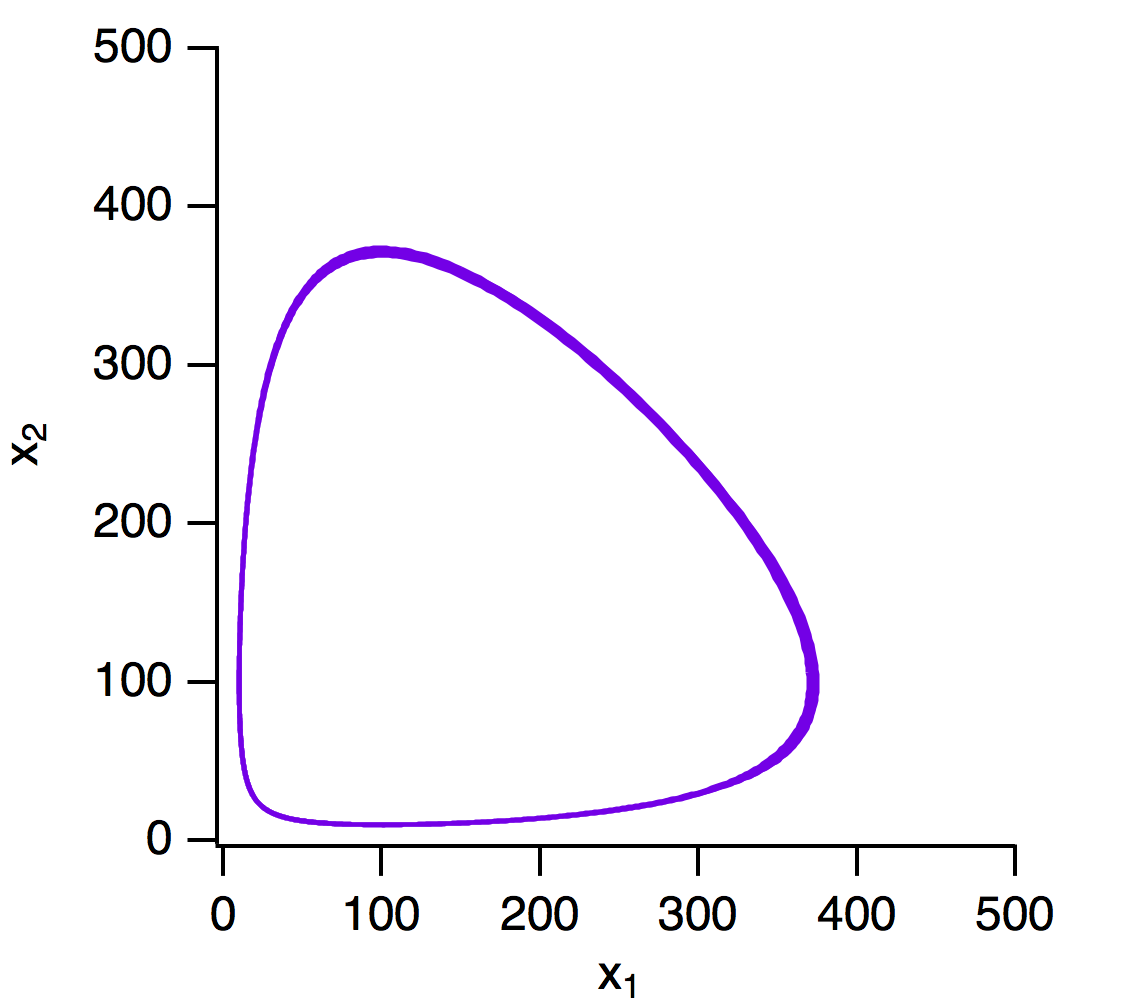
初期値を平衡点（(100, 100)）に近い点(99, 99)とすると下図のように円に近い軌道を描きます．

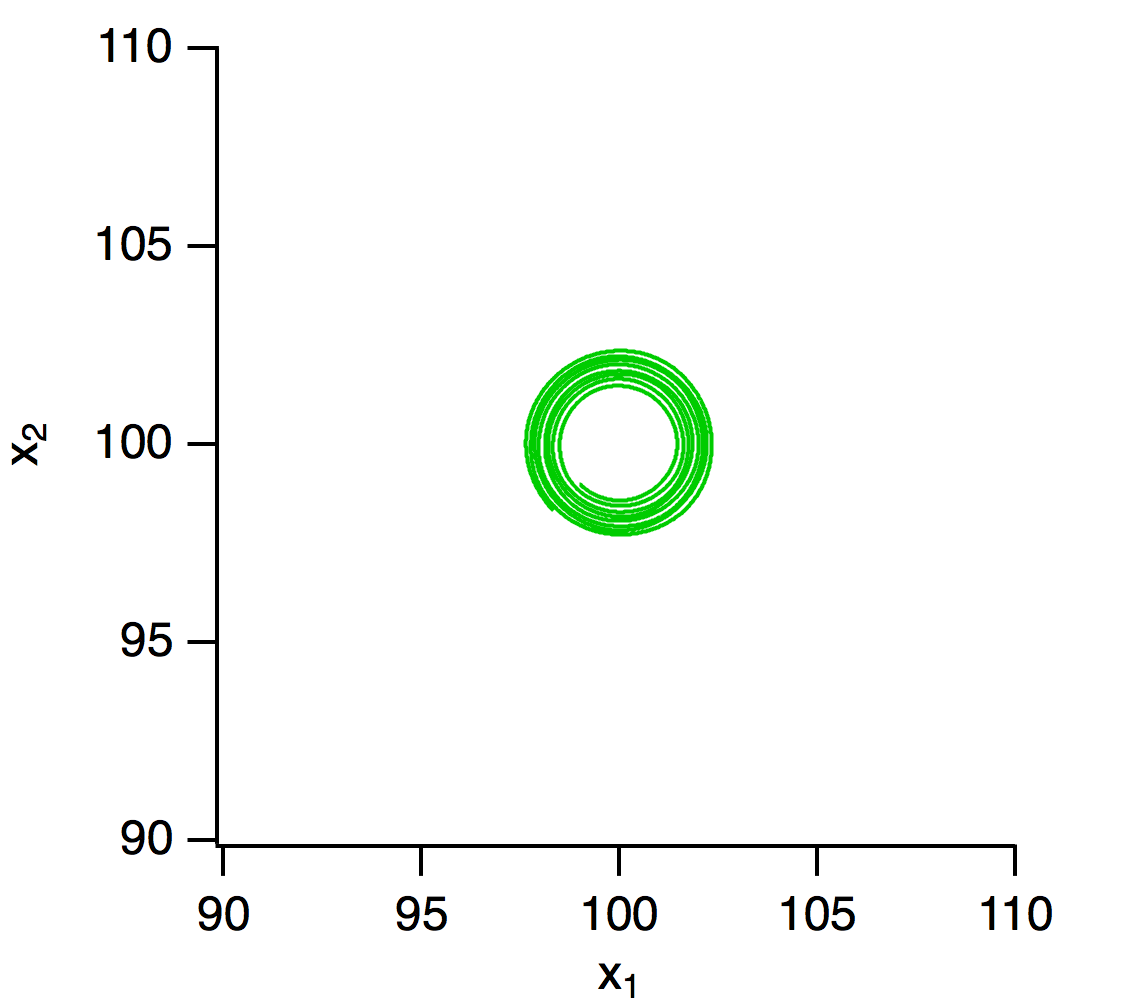
MATLABのコードです．

• lv.m

tspan = [0:0.001:5];
[t y] = ode45(@LotkaVolterra,tspan, [99 99]);
figure(1);
plot(t, y(:,1), 'b', t, y(:,2), 'r');
figure(2);
plot(y(:,1), y(:,2));

• LotkaVolterra.m

function dx = LotkaVolterra(t, x)
alpha = 10;
beta = 0.1;
gamma = 10;
delta = 0.1;
dx = zeros(2,1);
dx(1) = alpha * x(1) - beta * x(1) * x(2);
dx(2) = delta * x(1) * x(2) - gamma * x(2);
end

4年生と堀助教の歓迎会でした．いつもの焼肉です．