日吉キャンパスの銀杏が色付いてきました。例年より少し早いようです。
blog
バイオメカニズム学会奨励賞
Medical & Biological Engineering & Computing
木星
研究室合宿
虹
湘南藤沢高等部の理工学部見学会
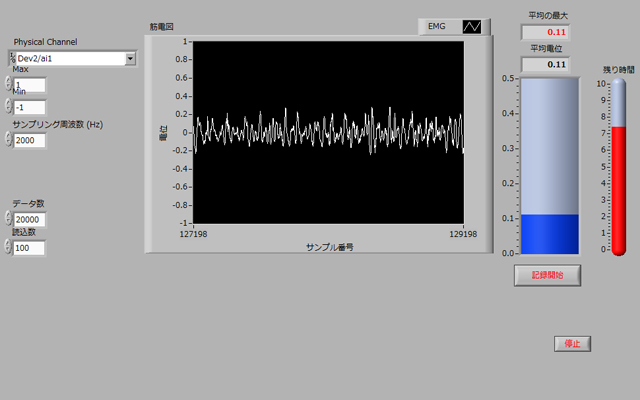
今日は湘南藤沢高等部の理工学部見学会でした。当研究室は見学コースの一つでした。見学会のときには,筋電図と筋音図の説明の後,計測のデモンストレーションを行います。筋電図の計測では,見学グループ毎に代表者1名に最大努力時の値を記録します。筋電図は絶対値を求めて一定時間の平均値を求めたものを指標にします。前のグループより大きな値がでると盛り上がります。
筋電図の波形をプロジェクタでスクリーンに投影すると同時に,アンプを通してスピーカから音としても確認できるようにしています。筋電図の周波数は表面電極で計測すると10〜1000 Hz程度なので,音としては低いですが,視覚と聴覚の両方で体験できるので,デモンストレーション向きです。一方,筋音図は「音」とは名ばかりで100 Hz以下の振動なので音として体験するには低くてデモンストレーションには向きません。
第1人称代名詞
某学会では,第1人称の「I」と「We」を使わないとしているようです。使用する頻度が高くないことは事実でしょうが,第1人称代名詞の使用の可否についての意見は一律ではないそうです[1]。
■回避すべき使用方法[1]
- 自信がないときの「I think〜」や「I believe〜」
- 物語のように説明する
- 読者が繰り返す必要がある行為を表す動詞(measure, calculateなど)の文
■適切な使用方法[1]
- 強い表現を弱くするとき
- 筆者に固有の行為を示す動詞(show, agreeなど)の文
[1] Kate L. Turabian著, 沼口隆,沼口好雄 訳,シカゴ・スタイル 研究論文執筆マニュアル,慶應義塾大学出版会(2012),pp. 166–168
学科パンフレット
8月のオープンキャンパスから新しい学科のパンフレットを配布しはじめました。下のパンフレットの写真は学科のweb pageに掲載したものです(こういう写真も私が撮影します)。
パンフレットの表紙がなかなか決まらず,私が作成した案をいくつか業者に提示しました。
この案は,卒業式のときの集合写真を使ったもので,格調高い感じがします。パンフレットにすると顔がはっきりわかるので,今回は見送りました。
2つめは学科のロゴとその鏡像を大きく使ったものです。
3つめは,4つの研究分野と2つの教育分野の文字をつかったものです。
実際のパンフレットは2つめと3つめを融合させたデザインになりました。
業者に提示することをしなかった案も10枚以上作りました。アイデアを形にしてみたものの,私の中で全く納得できないものでした。
学内学事発表用スタイルファイル
卒業研究発表会などの要旨の様式を作って使っていました。今回,4年生の必修科目のプレゼンテーション技法の発表会用に,要旨のLaTeXのスタイルファイルが欲しいとのことで,当研究室で使っていたものをベースに,先にリリースされたWordの様式に近くなるように修正したものを提供しました。
- 余白
- 上下左右の余白は20 mmです。余白の基準値は1インチ,つまり25.4 mmなので,左の余白を-5.4 mmにします。A4の幅は210 mmなので,右の余白を20 mmにするためにはテキストの幅を 210 – 20 × 2 = 170 mmにします。上と下も同様で,上の余白は-5.4 mmでテキストの高さを 297 – 20 × 2 = 257 mmにします。
\oddsidemargin -5.4mm \evensidemargin -5.4mm \textwidth 170mm \topmargin -5.4mm \headheight 0pt \headsep 0pt \textheight 257mm
- 段間の幅
- 2段組のときの間の幅が10 mmです。
\columnsep 10mm
- 書体と文字サイズ
- 日本語の題目は角ゴシック体14 pt,英語の題目はサンセリフ体12 pt,著者名は明朝体10 pt,英文のアブストラクトはセリフ体9 pt,本文は明朝体9 pt,節見出しは角ゴシック体/サンセリフ体9 pt,図と表のキャプションは明朝体/セリフ体9 ptです。
サンセリフ体とは,HelveticaやArialのように「ひげ」がない書体のことです。セリフ体はTimes系の書体のように「ひげ」がある書体のことです。デフォルトの行間を含めて再定義します。行数が48行なので,組版結果をみながら,\normalsizeの行間を14.2 ptにしました。文字サイズの1.5倍程度の行間にすると読みやすいようです。\large, \Largeおよび\LARGEにそれぞれ10, 12および14 ptの文字サイズを割り当てました。タイトルになるLargeとLARGEの行間は本文のそれより狭くしました。\renewcommand{\normalsize}{% \@setfontsize\normalsize\@ixpt{14.2}} \renewcommand{\large}{% \@setfontsize\large\@xpt{15}} \renewcommand{\Large}{% \@setfontsize\Large\@xiipt{14}} \renewcommand{\LARGE}{% \@setfontsize\LARGE\@xivpt{18}} - 行どり
- 節の見出しは2行どりなので再定義しました。また,英数字をサンセリフ体に,和文をゴシック体にしました。
\renewcommand{\section}{\@startsection{section}{1}{\z@}% {1\Cvs \@plus.1\Cdp \@minus.1\Cdp}% {.1\Cvs \@plus.1\Cdp}% {\reset@font\normalsize\sffamily\gtfamily}} \renewcommand{\subsection}{\@startsection{subsection}{2}{\z@}% {1\Cvs \@plus.1\Cdp \@minus.1\Cdp}% {.1\Cvs \@plus.1\Cdp}% {\reset@font\normalsize\sffamily\gtfamily}} \renewcommand{\subsubsection}{\@startsection{subsubsection}{3}{\z@}% {1\Cvs \@plus.1\Cdp \@minus.1\Cdp}% {.1\Cvs \@plus.1\Cdp}% {\reset@font\normalsize\sffamily\gtfamily}} - 節番号の後ろの余白
- 半角幅にしました。
\def\@seccntformat#1{\csname the#1\endcsname\hskip .5zw} - 図や表の前後の余白
- キャプションも含めて詰めました。
\setlength\intextsep{0pt} \setlength\textfloatsep{0pt} \setlength\belowcaptionskip{5\p@} \setlength\abovecaptionskip{0\p@} - 参考文献リストの行間
- 本文より行間を詰めました。
\renewenvironment{thebibliography}[1] {\section*{\refname\@mkboth{\refname}{\refname}}% \list{\@biblabel{\@arabic\c@enumiv}}% {\settowidth\labelwidth{\@biblabel{#1}}% \leftmargin\labelwidth \advance\leftmargin\labelsep \setlength\itemsep{0.0zh}% \setlength\baselineskip{12pt}% \@openbib@code \usecounter{enumiv}% \let\p@enumiv\@empty \renewcommand\theenumiv{\@arabic\c@enumiv}}% \sloppy \clubpenalty4000 \@clubpenalty\clubpenalty \widowpenalty4000% \sfcode`\.\@m} {\def\@noitemerr {\@latex@warning{Empty `thebibliography' environment}}% \endlist}
他にも細かな見た目の修正がいくつかありますが,レイアウトに関してはこの位の修正でほぼWordのテンプレートに近くなります。
箇条書きの環境について,行間を詰めることは環境を定義すればできるのですが,ここでは再定義しないで,本文の箇条書きの環境の中に
\setlength\parsep{0pt}\setlength\itemsep{0pt}
を記述することにしました。
左は欧文がTeXのデフォルトの書体であるComputer Modernで組んだもの,右は\usepackage{times}でセリフ体をTimes Roman,サンセリフ体をHelveticaで組んだもの(実際には互換書体)。